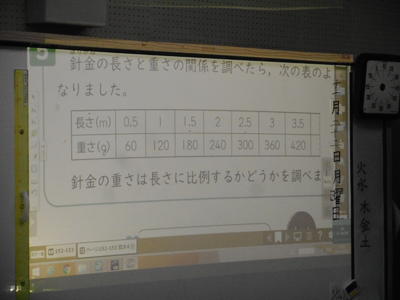
2021年11月の記事一覧
3年生 算数「暗算」
授業開始後の時間を活用して、復習をしました。タブレットの課題に取り組みました。
制限時間の中で集中して取り組みました。
答え合わせを兼ねて、クラスの様子を確認します。
大きな表示にして、確認しやすくしている児童もいます。
復習の答えの確認が終わりました。
めあて「かけ算を暗算でしてみよう。」
□ の中の数字を 1 とした時の 答えを暗算で出してみよう。
他の方法で解いた人はいますか?
①かける数の 4 を 十の位や一の位の数字にかけ算をする方法
②21を 20 と 1 に 分けて、それぞれかけ算をする方法
などが、出ましたね。 どちらの答えも 84 になります。
まとめ の確認をしました。
練習問題です。暗算で答えました。
答えは?・・・ 「75!」 正解です。
次は?・・・ 「72」 繰り上がりがあると、難しいですね。
教科書の練習問題を解きました。みんな集中しています。
今日も、みんなでがんばりました。
2年体育「ボール投げ遊び」
はじめのあいさつ
今日の予定確認
準備体操①(ラジオ体操)
準備体操②(サーキットトレーニング)
準備体操③(ボールを使った準備体操)
本時のめあて確認「さくせんをいかして、まとあてゲームをしよう」
1回戦
作戦タイム(クロムブックを活用して、守りをかわすために作戦をたてています。)
2回戦
後片付け
振り返り
終わりのあいさつ
たくさんの汗をかき、楽しく活動できました。
5年 算数「 面積 」
授業開始後の時間を活用して、既習内容の復習をしました。
制限時間が設けてあるので、集中しています。
終了の時間となり、答えの確認をしました。
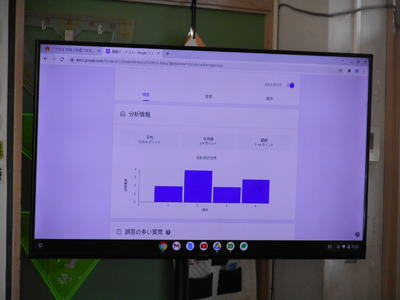
合計得点の分布も確認できます。
問題ごとの正誤の確認もでき、勘違いなどが原因で、誤答をしていることにも気づきました。
次は、計算問題(2問)をノートを使って解きました。
① 0.15✕0.3 ② 2.19 ÷ 1.8(商は少数第1位まで、あまりも出す)
制限時間を設け、答えの確認をしました。
いよいよ、面積の勉強に取りかかります。
前時の復習です。三角形の面積の求め方の確認をしました。(高さが底辺の外側にある場合)
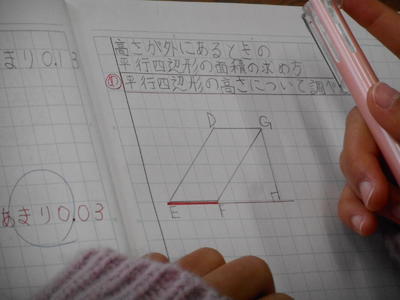
めあて「 平行四辺形の高さについて調べよう 」(高さが底辺の外側にある場合)
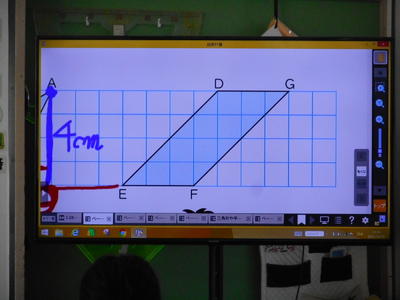
問題を確認した後、平行四辺形をノートに書いて、面積の求め方を考えました。
平行四辺形の「底辺」と「高さ」について、確認しました。
自分の考えを発表する場面でも、皆、積極的に取り組んでいます。
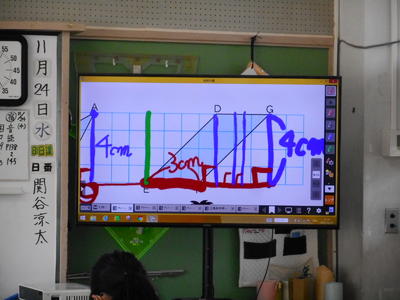
「底辺」が3cm 「高さ」が4cm であることが分かりました。
「平行四辺形」の「高さ」は、他にも・・・
児:「なるほど・・・」 「こんなに たくさんあるんだ・・・」
解き方を確認しました。
「高さ」が「底辺」の外側にある図形でも、図形を動かして一般的な平行四辺形にすることができる。
ということは、面積は、「底辺」 × 「高さ」で求めることができる。
つまり、「高さ」が「底辺」の外側にあっても、同じ方法で面積を求めることができる。
まとめ を確認しました。
練習問題を解きました。まず、図形をノートに書いてから計算をしました。

みんな、よく集中していました。
今日も、みんなで、一生懸命頑張りました。
4年 国語「伝統工芸の良さを伝えよう」
授業開始後の時間を活用して、日頃の音読について確認しました。
未習単元の音読を家庭学習で1周間ほどしています。
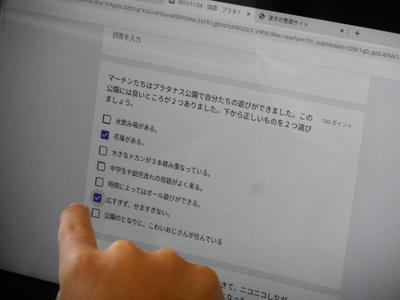
クロームブックを使って、内容について、質問事項に答えました。
児「あれ? どうだったかな?」 「意外とむずかしい!」
質問に沿って、どんどん入力しました。
入力が終わったら、集計のために送信します。
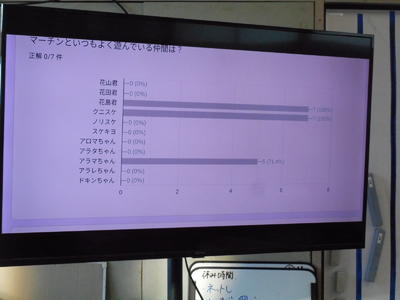
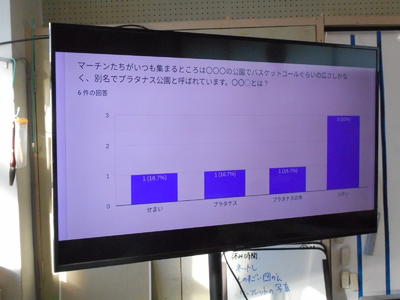
結果は、すぐに反映されます。全員が送信したら、みんなで確認しました。
音読をしながら、内容について、きちんと考える大切さを実感できました。
集計結果を見ながら、正しい内容について、みんなで確認しました。
先:「音読をするときにも、きちんと内容を理解しながら読めるといいですね。」
めあて 「リーフレットを完成させよう。」
早速、パンフレット仕上げに入りました。参考資料で引用した、ホームページのアドレスも転記します。
作業が進んでいる人は、先生に確認をしてもらいます。
ノートや、クロームブックで調べた内容などを参照し、リーフレットを作成しています。
写真を貼って、色をつけて見やすくするなどの工夫をすれば、間もなく完成です。
ふり返りを入力しました。
今日もみんなで、集中して学習に取り組めました。
6年 算数「比例と反比例」
開始後すぐに、前時の授業の復習、確認をしました。
学習プリントが返却され、間違えたところは教え合いで確認しました。
間違えやすい問題について、解説を聞きながら、確認しました。
前時の授業の記録から、比例になる場合と比例にならない場合について確認しました。
比例の場合の例(1袋 280円の トマトの袋の数 と 値段 の関係)
比例にならない場合(自分 と 弟 の年齢の関係)
比例の場合は、2つの数の関係で、片方の数が2倍3倍になる時、
それにともなって、もう片方の数も2倍3倍になる関係のこと。
本時の課題:「比例する関係を式に表すこと」を確認しました。
めあて「比例する2つの数を X と y を使って式に表そう。」
自分の考えがまとまったら、近くの人と確かめ合いをしました。
2通りの標記のしかたが出てきました。
① y=2 × X ② y= X × 2
問題の意味を分かりやすくしているのは、 ① であることに気づきました。
話し合ったことを 言葉にして、まとめとしました。
確かめ問題と練習問題を解きました。
先生に 正解の〇をつけてもらい、理解できた人は、ともだちへの助言や丸付けをします。
みんな、〇がもらえました。
ふり返りをノートに記入し、ドリルの問題で力試しをしました。
問題を解き終えた人は、ドリルを提出しました。
今日もみんなんで力を合わせて、頑張りました。